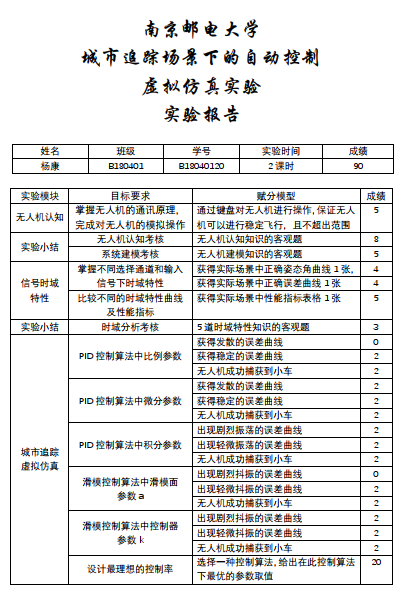
实验要求
1. 专业与年级要求
主要面向自动化、测控技术与仪器、智能科学与技术、物联网技术等电子信息类专业大三年级学生。
2. 基本知识和能力要求
学过《自动控制原理》本实验是专业课的课程实验,需要有一定的高等数学、信号处理、自控原理及算法的知识基础。
教学成果
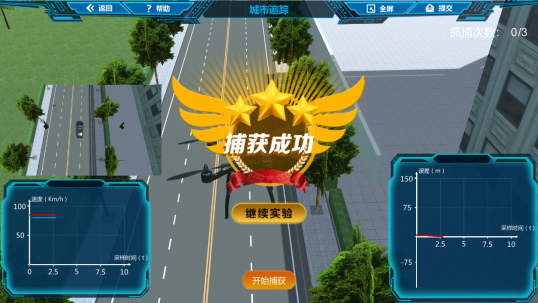
实验背景
通过综合创新实验,使学生能够更好地了解、熟悉、掌握旋翼式无人飞行器的基本组成、工作原理、动力学特性及数学建模,并以此巩固二阶系统的时域响应和频域响应知识点,能够设计并验证PID控制及其它控制算法。通过无人机追踪实际应用场景,反应出自动控制理论与实际系统之间的内在关系,学生可以更好的设计参数实现飞机良好追踪。
设计原则
1.实验原理
本实验项目的技术思想来源于国家智慧城市行业的迫切需求,针对无人机追踪肇事逃逸车辆问题,分别对无人机系统,逃逸车辆系统进行分析、建模。把城市追踪问题转换为控制问题里面的校正问题。结合控制理论,分析系统,设计合适的控制策略,实现最终的追踪任务。

图7 城市追踪应用场景
(1)模型
飞机模型:
四旋翼无人机是一个复杂的动力学系统,为具有多输入多输出,强耦合的欠驱动系统,其受力分析如图8所示。

图8 四旋翼无人机受力分析
将无人机视为一个刚体,进行动力学分析,得到如下的数学模型:
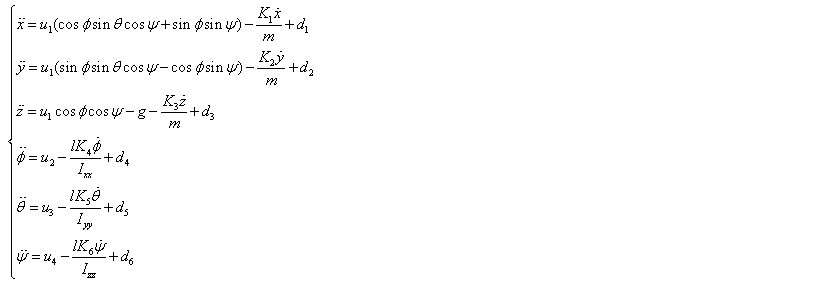
暂取x方向的位置状态进行分析,得到如下的系统方程:

其中,(x,y,z)为无人机质心在惯性坐标系中的位置坐标;k为阻力系数;x为x轴方向的位置;d=d1为系统噪声信号。
设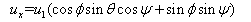 为虚拟控制输入,则四旋翼无人机x方向的位置状态方程变为:
为虚拟控制输入,则四旋翼无人机x方向的位置状态方程变为:

小车模型:
将小车模型视为一个二阶系统,进行动力学分析,得到如下的数学模型:

其中(xd, yd)为小车位置坐标。暂取x方向的位置状态进行分析,得到如下的系统方程:

误差系统:
为了实现城市追踪,取无人机和小车的x方向的位置误差为

则系统方程变为

(2)控制策略
PID控制策略:
PID控制的原理框图如图9所示:

图9 PID原理框图
使用PID控制策略设计控制律为:
其中Kp为比例系数,Ki为积分系数,Kd为微分系数。
PID控制的各部分有以下的作用:
a) 比例部分决定控制作用的强弱
b) 积分部分能消除稳态误差
c) 微分部分能够加快系统的调节过程
根据PID控制原理,此控制律可以使四旋翼无人机跟踪上小车。
滑模控制策略:

图10 滑模控制原理示意图
滑模控制分为两个阶段,第一个阶段是系统状态从滑模面外到达滑模面s=0,第二个阶段是系统状态沿着滑模面运动,最终到达平衡点。
取滑模面为:

其中,e=xd-x,![]() 是设计参数,xd是小车的位置
是设计参数,xd是小车的位置
则:

选取控制律为:

则:

其中,b是设计参数。因此,根据滑模控制原理,此控制律可以使无人机跟踪上小车。
实验内容涉及到的主要知识点:共 8个
① 多旋翼无人飞行器位置动力学特性认识;
② 多旋翼无人飞行器系统的组成与建模;
③ 二阶系统的时域特性分析;
④ 超调量、稳态误差、峰值时间、调节时间的认识;
⑤ PID控制原理;
⑥ 滑模控制原理;
⑦ PID控制器的参数整定;
⑧ 滑模控制器的参数整定。
实验目标
本实验教学以立德树人为根本任务,紧密围绕南邮大信息办学特色,基于自动控制的前沿技术,将实际复杂工程控制问题和虚拟仿真信息化技术相结合,价值塑造、知识传授和能力培养多元统一,培养和提升学生解决控制领域复杂工程实际问题的能力。具体实验教学目标包括:
(1) 培养学生的社会责任感,激发学生奉献社会的情怀和使命感,培养学生严谨的研究态度和科学的工作方法;
(2) 掌握控制系统的工作原理和建模方法,具备综合运用自动控制原理等课程知识点,分析和理解复杂工程控制对象、控制要求以及系统建模的能力;
(3) 掌握控制系统的性能测试与分析计算的方法,具备完成控制系统的搭建、算法设计和验证的能力;
(4) 掌握根据工程实际需求对控制系统进行设计与调试的方法,具备探究性思维方式,提高分析和解决实际问题的能力以及自主创新实践能力。
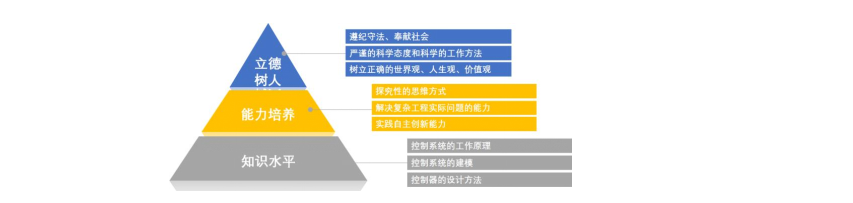
图6 实验教学目标
成绩评定